chiKR : XAFS振動をいじってみるプログラム

2018年11月22日、新登場!

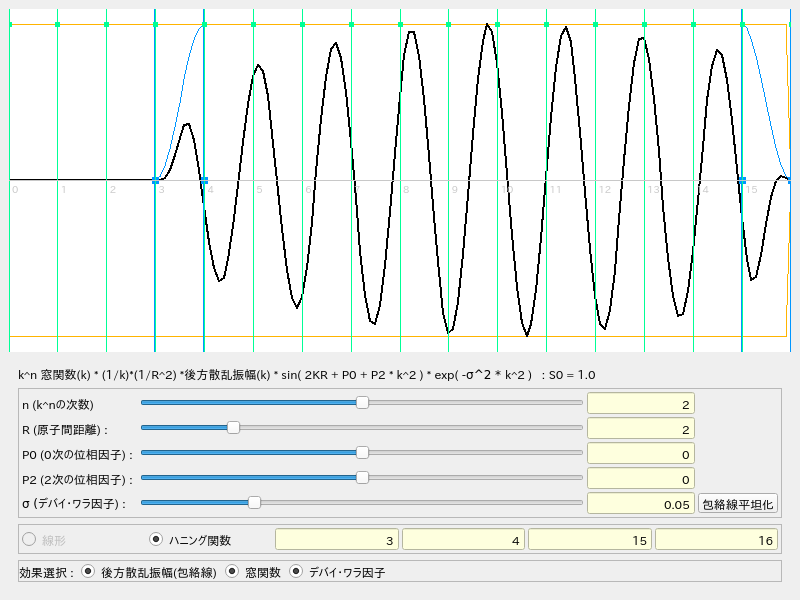
$\chi(k)$を構成する様々な因子(後方散乱因子、デバイワラ因子、位相因子)等をいじって$\chi(k)$の形を変え、
それによって、フーリエ変換結果($\chi(R)$)がどのように変化するかを体験的に実感してもらうことを目的にしたプログラムです。

chiKR には以下のような特徴が有ります。

  1. 後方散乱因子の形が変わると、フーリエ変換後のピーク形状はどう変わるか、後方散乱因子の形を山１つにしてみたり山2つにしてみたりして観察できます。
  2. デバイワラ因子の大きさが変わると、変換後のピークにどんな影響があるか観察できます。
  3. 窓関数は「打ち切り効果」を軽減すると言われますが、窓関数によって実際どのぐらい変換結果に影響が出るか(フリンジの出方が変わるか)観察できます。
  4. 振動因子 ($\sin(2kR+\phi(k))$ の $R$ を変えると、変換後のピーク位置がちゃんと変わります :-)
  5. 位相因子の 0次の項を変えるとどんな変化が出るかがわかります。$\chi(R)$ を見る時、絶対値だけではなく、実部・虚部も見たほうが良い理由がわかります。
  6. 位相因子の 1次の項ははいってません。 $R$ を変えるのと同じ効果しか無いからです。
  7. 位相因子の 2次の項がほんの少し入るとかなり劇的な効果を生みます。変換後のピーク形状を非対称にしているのは、2次も含めた高次の(あるいは$k^{n}$の項の)効果です。

○ $\chi(k)$ をいじってみるウインドウ。

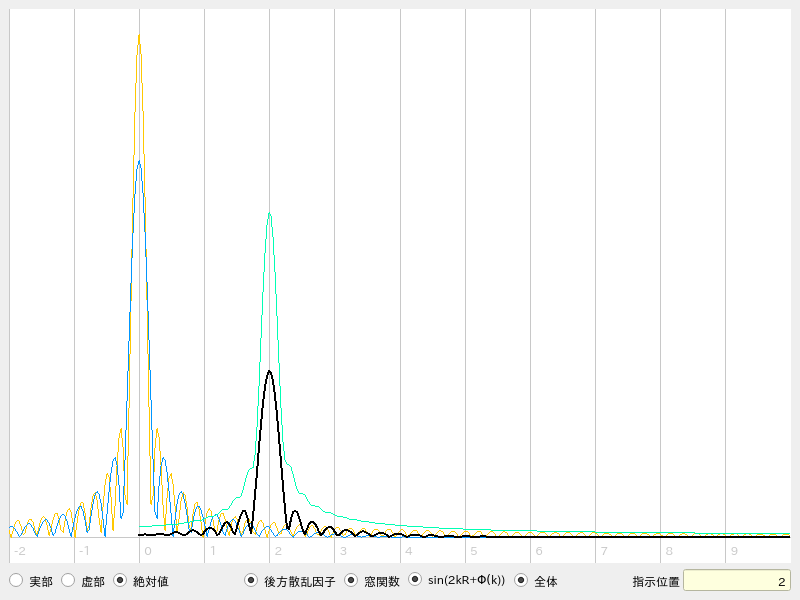
○いじった $\chi(k)$ をフーリエ変換して得られる $\chi(R)$ の様子を眺めるウインドウ。

履歴

  1. 2018.11.22 : 公開を始めました。
  2. 実行ファイル (Windows版, 2018.12.04) 見栄えを少し改善。実行に必要なライブラリ等を含まない実行ファイル単独ですので、まず 2018年11月22日版の zip ファイルを解答し、その中にある exe ファイルを置き換えて下さい。

当 web ページとその下のページに関するお問い合わせ等ございましたら、連絡先にご連絡をお願いします。
田渕のページのルート